二元樹（Binary Tree）是一個常見且重要的樹狀結構，由有限節點組合而成的集合，此集合不是空集合，就是由樹根、左子樹和右子樹所組成，意思就是二元樹的分支度會小於或等於2，最多只會有兩個子節點。

二元樹和一般樹的差異：

1. 二元樹可以為空集合，而一般樹至少由一個節點組成。
2. 二元樹有次序關係，而一般樹則沒有。
3. 二元樹的節點分支度（d）為0 ≦ d ≦ 2，而一般樹的節點分支度為 0 ≦ d。
   

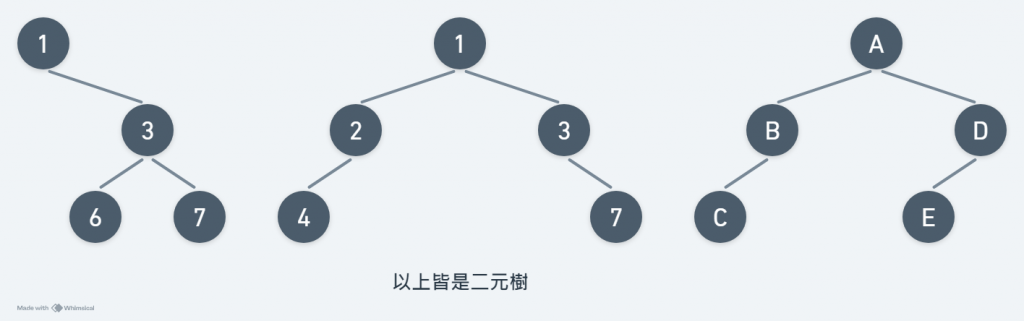
特殊二元樹

1. 完滿二元樹（Full Binary Tree）

   假設完滿二元樹的高度為 h，則樹的節點樹為 2h-1，h ≧ 0，換句話說，除了葉節點以外，每個節點都會有兩個子節點。

   如圖所示：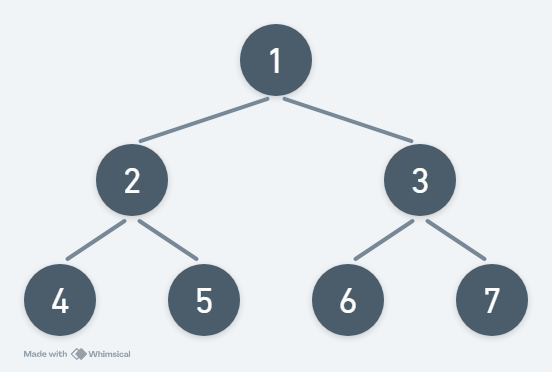
   

2. 完整二元樹（Complete Binary Tree）

   假設完整二元樹的深度為 h，則所含的節點數小於 2h-1，且其節點如完滿二元樹從左至右，由上到下的順序編號。

   如圖所示：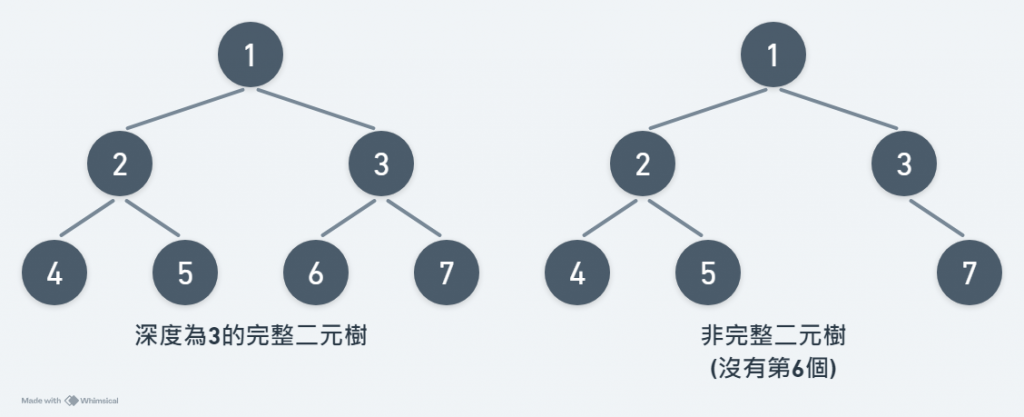
   

3. 歪斜樹（Skewed Binary Tree）

   如果二元樹完全沒有右節點或左節點時，分別叫做左歪斜樹和右歪斜樹。

   如圖所示：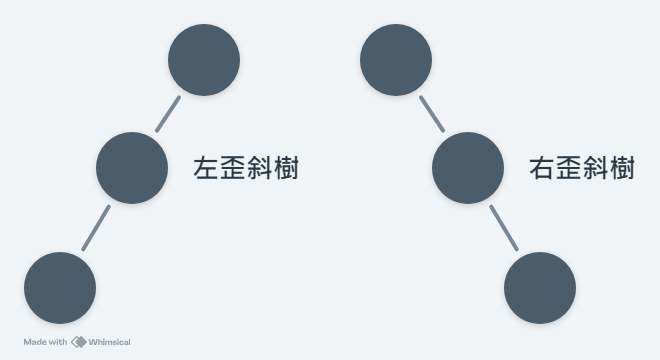
   

4. 嚴格二元樹（Strictly Binary Tree）

   嚴格二元樹除了葉節點都有非空的左右子樹，也就是沒有一個節點只有一個子節點。

   如圖所示：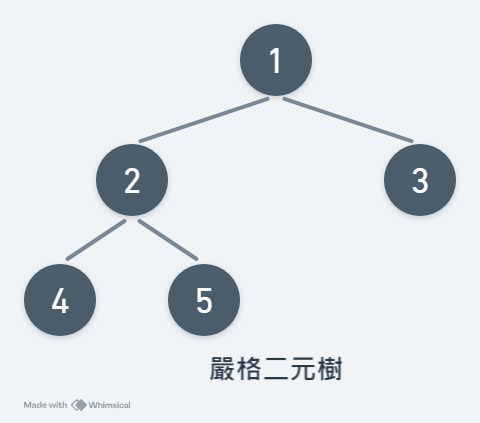
   

二元樹儲存方法

1. 一維陣列表示法

   首先將二元樹假想成一個完滿二元樹，並依序存放在一維陣列中。

   如圖所示：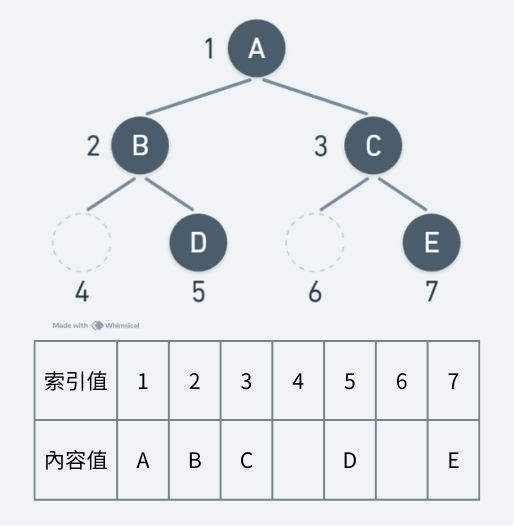
   

   優點：

   • 存取速度較快：可以根據索引快速訪問節點及其子節點。
   • 不須為每個節點額外分配指標，只需一個陣列即可。

   缺點：

   • 如果樹的結構不完整，陣列中會有大量未使用的空間造成浪費，尤其是對於大型但稀疏的樹狀結構。
   • 對於節點的新增與刪除比較麻煩，必須重新建立二元樹。

2. 串列表示法

   每個節點可以含有兩個指標，使用指標分別指向左邊子節點及右邊子節點。

   如圖所示：

   

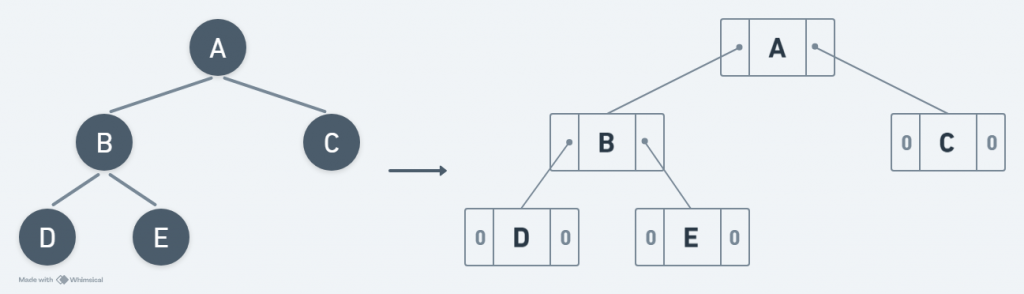
   優點：

   • 只有實際存在的節點占用記憶體，不會造成節點空間浪費。
   • 因為可以直接操作指標，所以對於節點的新增與刪除相當容易。

   缺點：

   • 每個節點需要額外的指標來存儲左右子節點，增加了記憶體使用量。
   • 存取速度較慢，因為訪問節點需要通過指標遍歷，可能會比陣列的直接索引要慢。

二元樹走訪

二元樹的走訪目的在於拜訪樹中所有節點各一次，走訪的方法分為以下三種：

1. 中序走訪 (Inorder)：走訪左子樹 → 拜訪樹根 → 走訪右子樹

   沿著樹的左側路徑移動，直到無法移動，再追蹤此節點，然後向右移動一節點。走訪完右子樹則返回上層的父節點，並重複左、中、右的步驟進行，直到拜訪完所有節點。

2. 前序走訪 (Preorder)：拜訪樹根 → 走訪左子樹 → 走訪右子樹

   先拜訪根節點，再往左方移動，直到無法繼續，然後向右方移動，並重複此步驟進行，直到拜訪完所有節點。

3. 後序走訪 (Postorder)：走訪左子樹 → 走訪右子樹 → 拜訪樹根

   先往左方移動，直到無法繼續，然後向右方移動，最後再處理根節點，並重複此步驟進行，直到拜訪完所有節點。

範例：

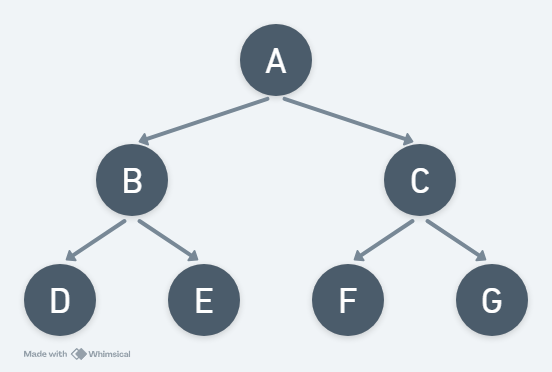
中序走訪順序：DBEAFCG

前序走訪順序：ABDECFG

後序走訪順序：DEBFGCA

參考資料：

1. 蔡明志 (2017)。《資料結構：使用C語言 (第5版)》。臺北：全華圖書。
2. 吳燦銘、胡昭民 (2018)。《圖解資料結構：使用Java》。新北：博碩文化。